the Tapestry Model

a generalization of Object Oriented Programming

Claim: The tapestry model offers to deepen our understanding of object oriented programming (OOP) through a generalization of the notion of a class.

model overview

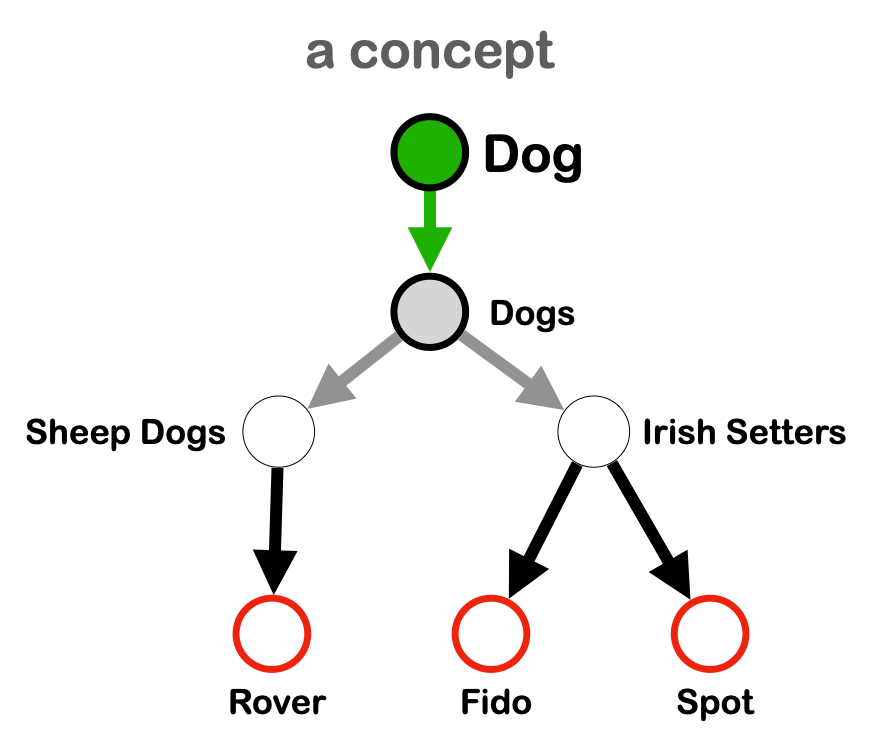
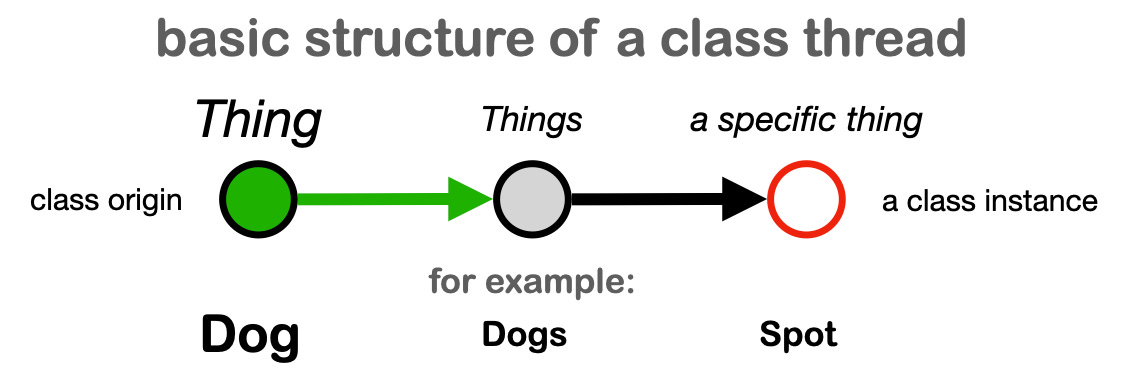
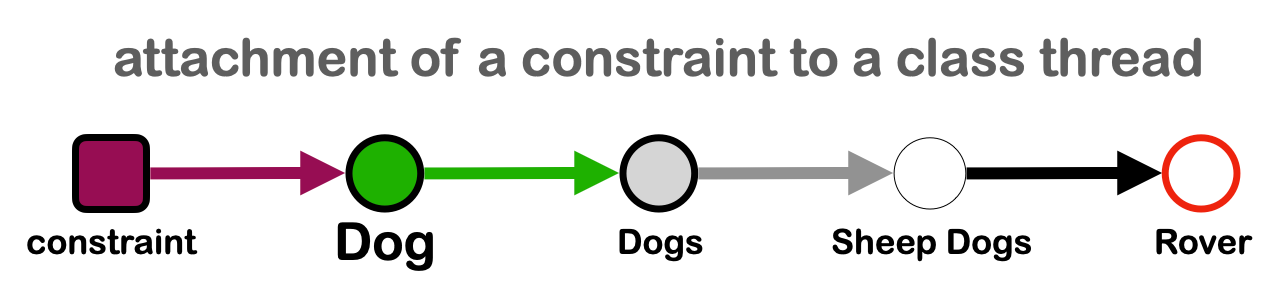
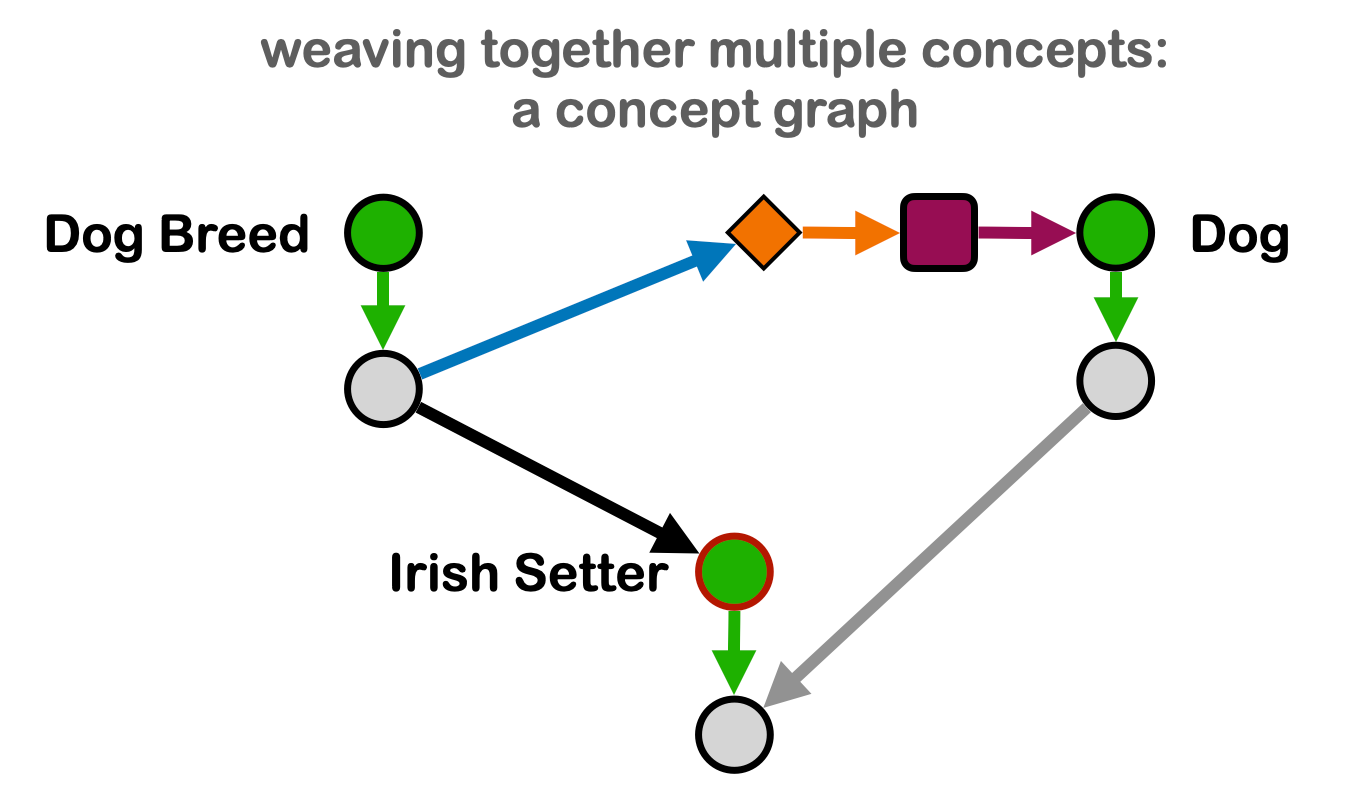
The tapestry model of knowledge representation begins with the idea of a class thread as the organizing principle of a graph.

Fig 1: Knowledge is represented as a graph, with nodes and edges. Nodes can represent any chunk of data, regardless of physical form (e.g. a digital file, piece of paper, patch of neurons), format (json, jpeg, etc), or size.

Fig 2: A class thread. The purpose of a class thread is to connect a specific thing to the abstract idea of a Thing. The simplest class thread contains only two edges and three nodes, as above.

Fig 3: The class thread from the previous figure with the addition of a subset node. Class threads are defined in terms of their three edge types: thread initiation (green arrow), propagation (grey arrow), and termination (black arrow). Any number of propagation edges are allowed, including zero.

Fig 4. The set of all class threads emanating from a class origin defines a concept.

Fig 5: The constraint node (far left) provides formatting information for the class instance (far right) and serves a role analogous to that of variables and methods of a class in OOP.

Fig 6: A concept with a JSON schema as a constraint node. Files of each of the 3 red circles must validate against the constraint node.

Fig 7: The property tree corresponding to the JSON schema in Fig 5. Property trees can be of any arbitrary depth and complexity.

Fig 8: Horizontal integration of two concepts. The array of instances on the left defines the allowed values of the property on the right.

Fig 9: Three types of concept integrations are depicted, two vertical and one horizontal. The integration between Dog and Irish Setter is equivalent to class inheritance in OOP. Dog Breed and Dog are horizontally integrated. Horizontal integration does not have a natural counterpart in OOP. (Is this a fair statement?)

Fig 10: Decomposition of the formatting specifications of a more complex object into a property tree. Properties of type: object, such as contactInfo, can have child properties in the property tree, which provide the opportunity for more extensive horizontal integration.

summary

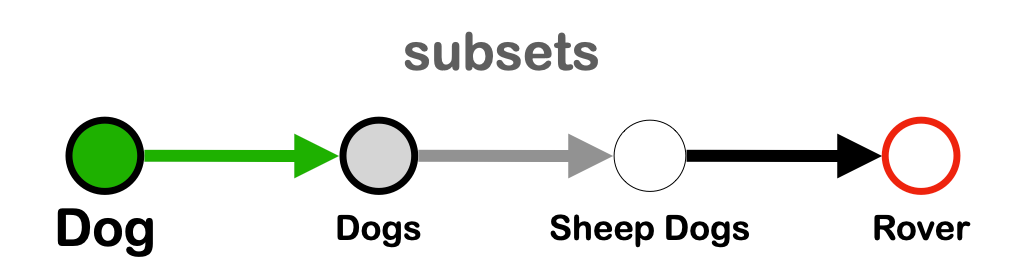
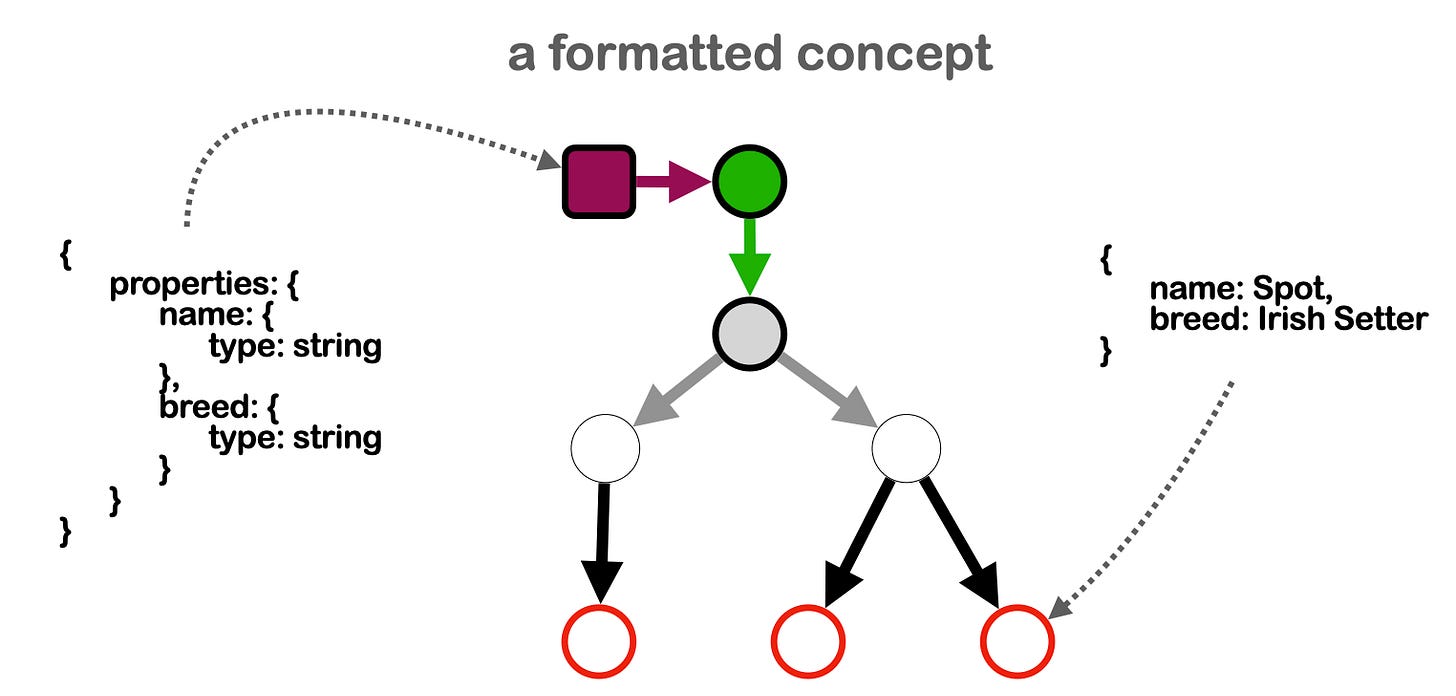
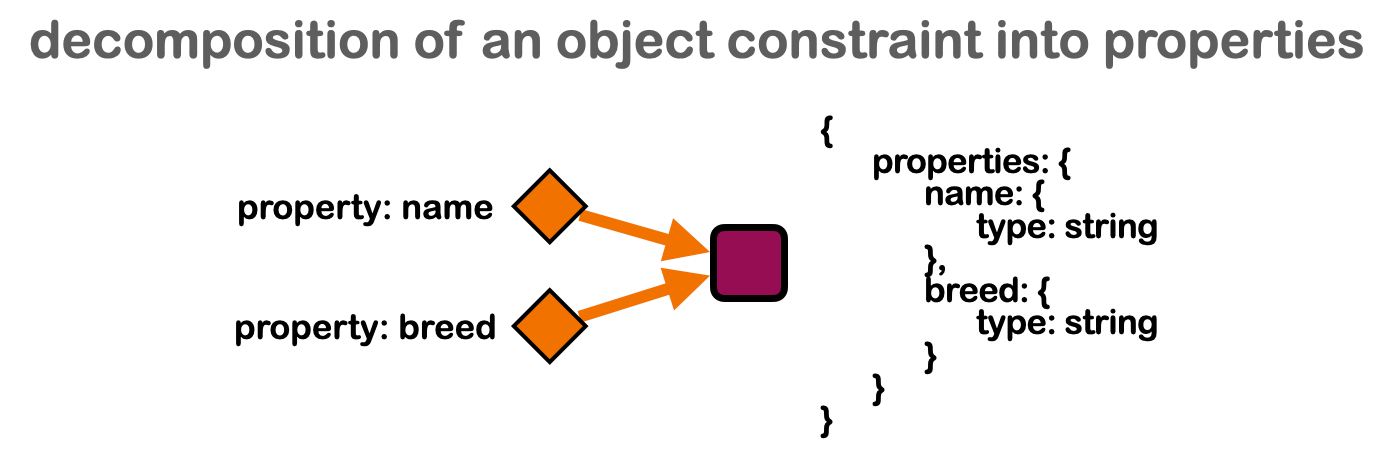
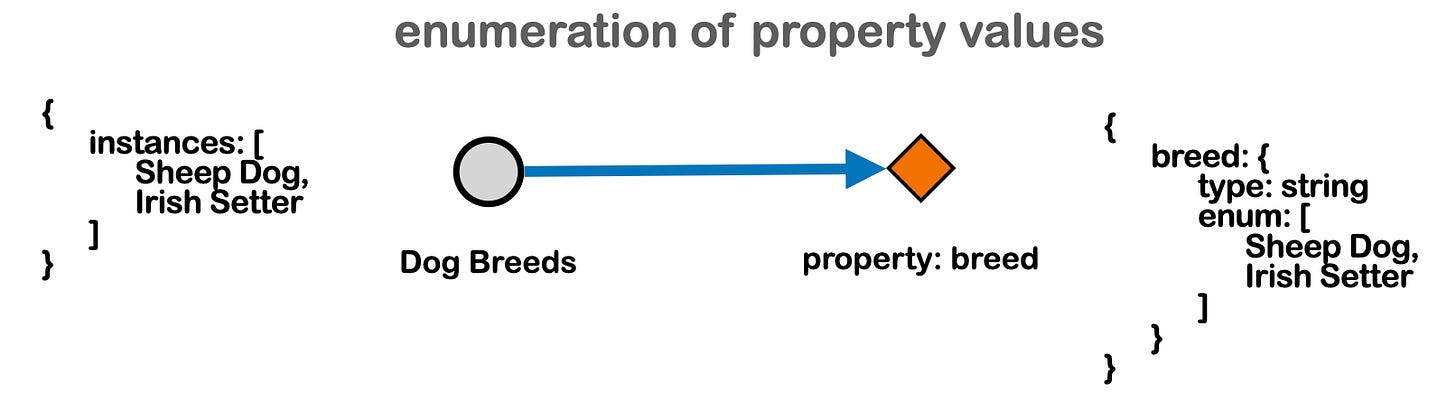
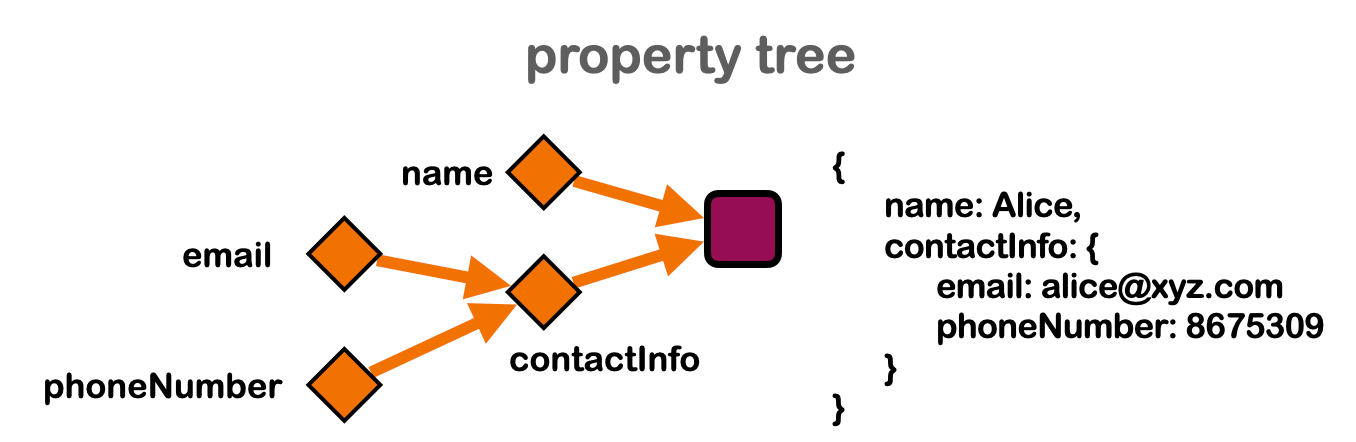
The tapestry model is based on the use of class threads as the organizational principle of knowledge in a graph. This allows us to define and organize data into concepts (Fig 4). Three methods to join concepts together are offered (Fig 9), only one of which has a natural counterpart in object oriented programming.

Compared to OOP, the tapestry model relaxes the requirement that classes produce objects. But we discover that objects are preferred because they enable extensive horizontal integration in addition to the vertical integration already enabled by OOP through class inheritance.

Benefits of the tapestry model include:

• more extensive and detailed integration of ideas and concepts

• an improved theoretical understanding of OOP

The following definitions may be useful to develop the tapestry model further:

• orphan node: a node that is not the instance of any unconstrained class thread in the graph; may also be referred to as unformatted or unconstrained

• a graph with at least one orphan node is an unconstrained

• a graph with no duplicated nodes is normalized.

• a fully integrated graph is one in which the process of breaking constraints into properties and forming horizontal integrations has been pursued to the maximum possible extent.

• conceptualization: the process of representing any given piece of data as a graph using the tapestry model

Academic areas of interest may include:

• research into the relationships between data storage inside individual nodes versus topologically encoded data. The process of querying the graph for topologically encoded data, such as a list of a concept’s instances, and encoding it inside one or more nodes may be referred to as expansion of the data. The reverse process, i.e. editing individual nodes to excise data that is already encoded topologically, may be called compactification of the graph. A concept graph is compact if compactification has been pursued to the maximum extent possible.

• mathematical properties of fully compact, fully normalized, fully integrated concept graphs

• methods and implications of combining nodes of mixed physical form within the same concept graph (e.g. digital with neuronal nodes)

These benefits should motivate the construction of tools to facilitate conceptualization of wide categories of data by everyday users in addition to computer scientists.